library(phyloseq)
library(vegan)
ps <- readRDS("data/moving-pictures-ps.rds")Ordination Plots
Ordination reduces a complex community table into a small number of axes that summarize between-sample dissimilarity.
The goal is not to compress biology into two numbers. The goal is to visualize structure, then interpret it cautiously.
This chapter focuses on:
- Bray–Curtis distance and why it is common
- PCoA ordination and what the axes mean
- how to read clustering and overlap
- how to avoid common interpretation traps
Load data
Transform to relative abundance
Bray–Curtis is commonly applied to relative abundance in exploratory ordination. This does not remove compositional constraints, but it enables clearer comparison across samples.
ps_rel <- phyloseq::transform_sample_counts(ps, function(x) x / sum(x))Compute Bray–Curtis distance
dist_bc <- phyloseq::distance(ps_rel, method = "bray")
dist_bc L1S105 L1S140 L1S208 L1S257 L1S281 L1S57 L1S76
L1S140 0.6861838
L1S208 0.6354987 0.3372080
L1S257 0.6768454 0.4388476 0.2702215
L1S281 0.7195914 0.3990832 0.2594049 0.2955335
L1S57 0.3106120 0.7252243 0.7422412 0.7606517 0.7471986
L1S76 0.2863643 0.7120062 0.7159927 0.7417853 0.7207266 0.2189226
L1S8 0.4512654 0.6795777 0.7973102 0.8243985 0.8599067 0.3791323 0.3615239
L2S155 0.9909207 0.9947296 0.9953983 0.9968108 0.9983371 0.9945933 0.9956765
L2S175 0.9909995 0.9961843 0.9958106 0.9972231 0.9986320 0.9957774 0.9963520
L2S204 0.9849699 0.9921312 0.9914588 0.9922580 0.9936669 0.9858092 0.9863838
L2S222 0.9780206 0.9899924 0.9920639 0.9926342 0.9906414 0.9862469 0.9821148
L2S240 0.9987646 0.9955455 0.9964632 0.9990941 0.9994072 0.9988327 0.9994072
L2S309 0.9782157 0.9723896 0.9612015 0.9676636 0.9612403 0.9774489 0.9788584
L2S357 0.9879793 0.9929860 0.9917003 0.9931128 0.9945217 0.9880474 0.9886220
L2S382 0.9953728 0.9984643 0.9971786 0.9985911 1.0000000 0.9994254 1.0000000
L3S242 0.4805294 0.7271526 0.8252262 0.8516653 0.8850555 0.4064393 0.3737848
L3S294 1.0000000 0.9984643 0.9977920 0.9985911 1.0000000 0.9994254 1.0000000
L3S313 0.9825722 0.9898827 0.9926455 0.9940580 0.9954669 0.9894526 0.9900272
L3S341 0.9871516 1.0000000 0.9986506 0.9989042 1.0000000 0.9885655 0.9885655
L3S360 0.9962614 0.9834881 0.9827521 0.9823923 0.9834881 0.9969040 0.9969040
L3S378 0.7369703 0.2481115 0.3884257 0.4760457 0.4552850 0.7531227 0.7657090
L4S112 0.9841295 0.9895734 0.9911834 0.9925959 0.9940048 0.9868355 0.9874101
L4S137 0.9928269 0.9957148 0.9966694 0.9980819 0.9994908 0.9989163 0.9994908
L4S63 0.9915745 0.9917973 0.9971786 0.9985911 1.0000000 0.9994254 1.0000000
L5S104 0.9955097 1.0000000 0.9970559 0.9996869 1.0000000 0.9949351 0.9955097
L5S155 0.9950000 0.9950000 0.9920559 0.9946869 0.9950000 0.9944254 0.9950000
L5S174 1.0000000 1.0000000 0.9970559 0.9996869 1.0000000 0.9994254 1.0000000
L5S203 1.0000000 0.9976326 0.9946885 0.9973195 0.9976326 0.9994254 1.0000000
L5S222 1.0000000 1.0000000 0.9970559 0.9996869 1.0000000 0.9994254 1.0000000
L5S240 0.9993573 0.9944196 0.9923343 0.9941066 0.9944196 0.9994254 1.0000000
L6S20 0.9993573 0.9988330 0.9958889 0.9985199 0.9988330 0.9994254 1.0000000
L6S68 0.9993573 0.9991639 0.9962198 0.9988508 0.9991639 0.9994254 1.0000000
L6S93 0.9953728 0.9987056 0.9957615 0.9983925 0.9987056 0.9994254 1.0000000
L1S8 L2S155 L2S175 L2S204 L2S222 L2S240 L2S309
L1S140
L1S208
L1S257
L1S281
L1S57
L1S76
L1S8
L2S155 0.9907000
L2S175 0.9909489 0.5900299
L2S204 0.9821182 0.8136886 0.7987192
L2S222 0.9848453 0.7831451 0.7634378 0.7288398
L2S240 0.9940041 0.8953950 0.8455883 0.9479622 0.9426599
L2S309 0.9868822 0.6926222 0.5519007 0.7472176 0.7860768 0.8544109
L2S357 0.9836455 0.6700035 0.5397253 0.6763091 0.8207944 0.8174676 0.4116314
L2S382 0.9951316 0.7855241 0.7232100 0.8972879 0.8798106 0.8528749 0.7358669
L3S242 0.1485585 0.9874233 0.9876866 0.9882576 0.9908341 0.9893738 0.9824456
L3S294 0.9957344 0.3404962 0.6707680 0.8381657 0.8485564 0.9407977 0.7593781
L3S313 0.9850507 0.5850473 0.3144351 0.8244462 0.8191921 0.8483894 0.5192259
L3S341 0.9878546 0.7874072 0.7076779 0.4249104 0.8180087 0.8872448 0.6746743
L3S360 0.9969040 0.8555033 0.8496532 0.7097201 0.4929728 0.9459853 0.7706273
L3S378 0.7341648 0.9958178 0.9975981 0.9975981 0.9928915 0.9922015 0.9715234
L4S112 0.9820070 0.6706180 0.5194163 0.7157193 0.7715494 0.8009639 0.4297393
L4S137 0.9940877 0.7556410 0.5945486 0.8732522 0.8527641 0.7851720 0.6520813
L4S63 0.9963995 0.6760549 0.6739303 0.7356027 0.7028374 0.8947491 0.4526595
L5S104 0.9901066 0.8546264 0.8213260 0.9217288 0.9454032 0.4014934 0.8360600
L5S155 0.9895969 0.9006047 0.8442468 0.9632679 0.9576404 0.4471313 0.8833956
L5S174 0.9945969 0.9235950 0.8693045 0.9632679 0.9576404 0.5189250 0.9113859
L5S203 0.9945969 0.8647620 0.7941131 0.9518683 0.9448846 0.4275352 0.8499714
L5S222 0.9952925 0.9180795 0.8737022 0.9552545 0.9493104 0.4545292 0.8963598
L5S240 0.9945969 0.9130923 0.8561876 0.9556681 0.9475996 0.1356729 0.8621809
L6S20 0.9945969 0.9437228 0.9032973 0.9552305 0.9481993 0.3400844 0.9012498
L6S68 0.9945969 0.8880466 0.8440185 0.9479972 0.9397157 0.2119781 0.8352254
L6S93 0.9945969 0.8959667 0.8477541 0.9451642 0.9375584 0.4006562 0.8496055
L2S357 L2S382 L3S242 L3S294 L3S313 L3S341 L3S360
L1S140
L1S208
L1S257
L1S281
L1S57
L1S76
L1S8
L2S155
L2S175
L2S204
L2S222
L2S240
L2S309
L2S357
L2S382 0.7310140
L3S242 0.9828026 0.9902684
L3S294 0.7190127 0.8585569 0.9955407
L3S313 0.4918246 0.7499370 0.9845268 0.6315274
L3S341 0.5583873 0.8318545 0.9684986 0.8174127 0.7528730
L3S360 0.7687725 0.8798619 1.0000000 0.8984495 0.8760740 0.7345979
L3S378 0.9963339 0.9975981 0.7372373 0.9975981 0.9975981 0.9830451 0.9841822
L4S112 0.2575579 0.7019572 0.9833718 0.7322767 0.4975492 0.6043310 0.7654843
L4S137 0.5967539 0.4768818 0.9894574 0.8293720 0.6955663 0.7637356 0.8593176
L4S63 0.5408874 0.8090827 0.9919628 0.7465676 0.6184667 0.7375606 0.7788989
L5S104 0.8125098 0.8394030 0.9854762 0.9298766 0.8321425 0.8666115 0.9318885
L5S155 0.8637793 0.8641404 0.9849666 0.9542857 0.8198937 0.9116424 0.9618163
L5S174 0.8902437 0.8916929 0.9899666 0.9526531 0.8714097 0.9296200 0.9638803
L5S203 0.8296442 0.8178984 0.9899666 0.9264483 0.8123412 0.8979114 0.9534636
L5S222 0.8857399 0.8871409 0.9908559 0.9493130 0.8817394 0.9145939 0.9591203
L5S240 0.8263406 0.8625650 0.9899666 0.9526531 0.8628011 0.8962483 0.9417881
L6S20 0.8672378 0.8898494 0.9899666 0.9584025 0.9110211 0.9297369 0.9484772
L6S68 0.8072302 0.8238861 0.9899666 0.9398560 0.8646681 0.8714408 0.9451945
L6S93 0.8092837 0.8158719 0.9899666 0.9361907 0.8689997 0.8597575 0.9414717
L3S378 L4S112 L4S137 L4S63 L5S104 L5S155 L5S174
L1S140
L1S208
L1S257
L1S281
L1S57
L1S76
L1S8
L2S155
L2S175
L2S204
L2S222
L2S240
L2S309
L2S357
L2S382
L3S242
L3S294
L3S313
L3S341
L3S360
L3S378
L4S112 0.9975981
L4S137 0.9970889 0.5680203
L4S63 0.9962639 0.5068493 0.7707000
L5S104 0.9975981 0.8070114 0.7911794 0.9132800
L5S155 0.9925981 0.8430496 0.8207389 0.9220033 0.3778339
L5S174 0.9975981 0.8679552 0.8469996 0.9221059 0.5073626 0.4990604
L5S203 0.9952307 0.8051266 0.7738353 0.9145115 0.3362083 0.2053220 0.4396456
L5S222 0.9975981 0.8689426 0.8382419 0.9130828 0.4418247 0.3424239 0.3885819
L5S240 0.9920177 0.8194116 0.8028240 0.9055829 0.3809196 0.4451662 0.5493652
L6S20 0.9964310 0.8616005 0.8386636 0.9150477 0.6114991 0.6637454 0.6181351
L6S68 0.9967620 0.7963094 0.7640087 0.8968638 0.4620512 0.5587941 0.6122908
L6S93 0.9963037 0.7985092 0.7466046 0.8997108 0.5636800 0.6662455 0.5615285
L5S203 L5S222 L5S240 L6S20 L6S68
L1S140
L1S208
L1S257
L1S281
L1S57
L1S76
L1S8
L2S155
L2S175
L2S204
L2S222
L2S240
L2S309
L2S357
L2S382
L3S242
L3S294
L3S313
L3S341
L3S360
L3S378
L4S112
L4S137
L4S63
L5S104
L5S155
L5S174
L5S203
L5S222 0.2366401
L5S240 0.4458029 0.5049871
L6S20 0.5598046 0.5913625 0.3448338
L6S68 0.4859858 0.5030199 0.2389513 0.2872778
L6S93 0.5680773 0.5414293 0.4194497 0.4576859 0.3980151PCoA ordination
ord <- phyloseq::ordinate(ps_rel, method = "PCoA", distance = dist_bc)
# Coordinates for the first two axes
coords <- as.data.frame(ord$vectors[, 1:2])
colnames(coords) <- c("PC1", "PC2")
# Percent variance explained (if available)
eig <- ord$values$Relative_eig
var_pc1 <- if (!is.null(eig) && length(eig) >= 1) eig[1] * 100 else NA_real_
var_pc2 <- if (!is.null(eig) && length(eig) >= 2) eig[2] * 100 else NA_real_
meta <- data.frame(phyloseq::sample_data(ps_rel))
meta$sample_id <- rownames(meta)
coords$sample_id <- rownames(coords)
ord_df <- merge(coords, meta, by = "sample_id", all.x = TRUE)
# Robust body site column detection
cols <- names(ord_df)
body_col <- intersect(c("body-site", "body.site", "body_site"), cols)
if (length(body_col) == 0) {
stop("Body site column not found in metadata. Available columns: ", paste(cols, collapse = ", "))
}
ord_df$body_site <- ord_df[[body_col[1]]]
# Store variance labels for plotting
ord_df$pc1_label <- ifelse(is.na(var_pc1), "PC1", sprintf("PC1 (%.1f%%)", var_pc1))
ord_df$pc2_label <- ifelse(is.na(var_pc2), "PC2", sprintf("PC2 (%.1f%%)", var_pc2))
dir.create("outputs/tables", recursive = TRUE, showWarnings = FALSE)
readr::write_csv(ord_df, "outputs/tables/ordination-pcoa.csv")
# Save variance info (optional)
var_df <- data.frame(PC1 = var_pc1, PC2 = var_pc2)
readr::write_csv(var_df, "outputs/tables/ordination-variance.csv")
head(ord_df[, c("sample_id","PC1","PC2","body_site")]) sample_id PC1 PC2 body_site
1 L1S105 0.5304992 0.08234422 gut
2 L1S140 0.5307266 0.08936046 gut
3 L1S208 0.5185157 0.08949133 gut
4 L1S257 0.4958304 0.08236422 gut
5 L1S281 0.4923930 0.08187132 gut
6 L1S57 0.5167373 0.08345351 gutOrdination plot (Python)
This plot uses Python for a clean, modern visualization layer. It includes points, group centroids, and confidence ellipses.
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from matplotlib.patches import Ellipse
df = pd.read_csv("outputs/tables/ordination-pcoa.csv").dropna(subset=["body_site"])
# Palette customization
palette_name = "Set1" # Try: "Set1", "tab10", "colorblind", "viridis"
groups = list(df["body_site"].astype(str).unique())
palette = sns.color_palette(palette_name, n_colors=len(groups))
color_map = dict(zip(groups, palette))
sns.set_theme(style="whitegrid", context="notebook")
def add_confidence_ellipse(ax, x, y, n_std=1.96, **kwargs):
x = np.asarray(x)
y = np.asarray(y)
if len(x) < 3:
return
cov = np.cov(x, y)
if np.any(~np.isfinite(cov)):
return
vals, vecs = np.linalg.eigh(cov)
order = vals.argsort()[::-1]
vals = vals[order]
vecs = vecs[:, order]
theta = np.degrees(np.arctan2(*vecs[:, 0][::-1]))
width, height = 2 * n_std * np.sqrt(vals)
ell = Ellipse(
xy=(np.mean(x), np.mean(y)),
width=width,
height=height,
angle=theta,
**kwargs
)
ax.add_patch(ell)
# Axis labels with variance if present
pc1_label = df["pc1_label"].iloc[0] if "pc1_label" in df.columns else "PC1"
pc2_label = df["pc2_label"].iloc[0] if "pc2_label" in df.columns else "PC2"
fig, ax = plt.subplots(figsize=(8.5, 6))
# Points
sns.scatterplot(
data=df,
x="PC1",
y="PC2",
hue="body_site",
palette=color_map,
s=65,
alpha=0.85,
edgecolor="black",
linewidth=0.35,
ax=ax
)
# Centroids and ellipses
for g in groups:
sub = df[df["body_site"].astype(str) == g]
cx, cy = sub["PC1"].mean(), sub["PC2"].mean()
ax.scatter([cx], [cy], s=160, marker="X", edgecolor="black", linewidth=0.6, zorder=5)
add_confidence_ellipse(
ax,
sub["PC1"],
sub["PC2"],
n_std=1.96,
facecolor=color_map[g],
alpha=0.12,
edgecolor=color_map[g],
linewidth=1.2
)
ax.set_title("PCoA (Bray–Curtis distance)", weight="bold")
ax.set_xlabel(pc1_label)
ax.set_ylabel(pc2_label)
ax.axhline(0, linewidth=0.6, alpha=0.6)
ax.axvline(0, linewidth=0.6, alpha=0.6)
sns.despine(ax=ax)
ax.legend(title="Body site", bbox_to_anchor=(1.02, 1), loc="upper left", frameon=False)
fig.tight_layout()
plt.show()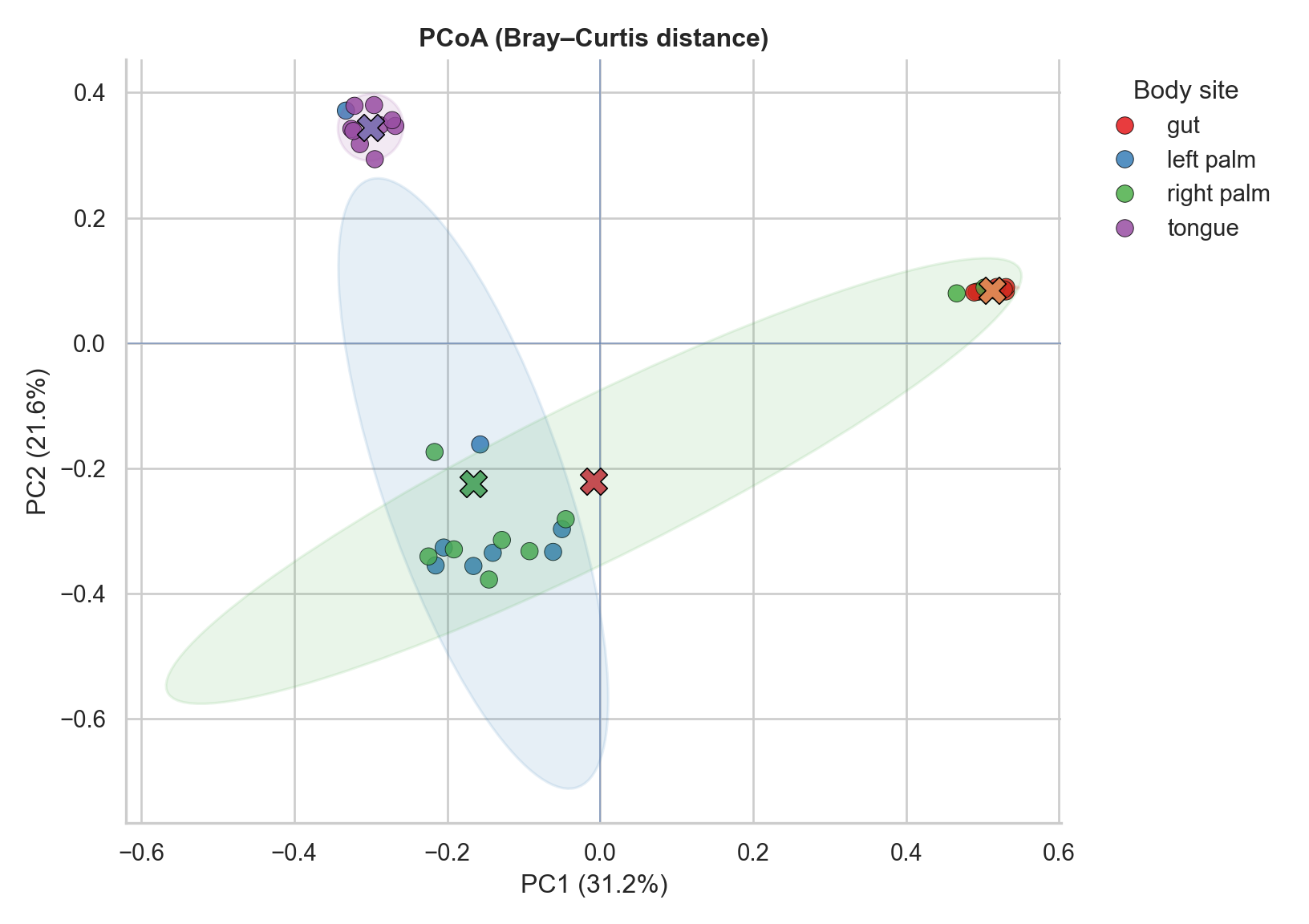
Reading the plot responsibly
What clustering can suggest
- Distinct clusters by group can indicate systematic differences in composition.
- Overlap can indicate weak separation or high within-group variability.
- A single outlier can stretch the geometry and distort visual separation.
What ordination does not tell you
- It does not identify which taxa drive separation.
- It does not prove statistical significance.
- It does not separate technical effects from biology.
Optional: PERMANOVA (group differences)
PERMANOVA tests whether group centroids differ in multivariate space.
meta_df <- data.frame(phyloseq::sample_data(ps_rel))
cols <- names(meta_df)
body_col <- intersect(c("body-site", "body.site", "body_site"), cols)
if (length(body_col) == 0) {
stop("Body site column not found for PERMANOVA.")
}
meta_df$body_site <- meta_df[[body_col[1]]]
vegan::adonis2(dist_bc ~ body_site, data = meta_df)Permutation test for adonis under reduced model
Permutation: free
Number of permutations: 999
vegan::adonis2(formula = dist_bc ~ body_site, data = meta_df)
Df SumOfSqs R2 F Pr(>F)
Model 3 5.2330 0.42437 7.3723 0.001 ***
Residual 30 7.0982 0.57563
Total 33 12.3312 1.00000
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Optional: dispersion check (beta dispersion)
meta_df <- data.frame(phyloseq::sample_data(ps_rel))
cols <- names(meta_df)
body_col <- intersect(c("body-site", "body.site", "body_site"), cols)
meta_df$body_site <- meta_df[[body_col[1]]]
bd <- vegan::betadisper(dist_bc, group = meta_df$body_site)
bd
Homogeneity of multivariate dispersions
Call: vegan::betadisper(d = dist_bc, group = meta_df$body_site)
No. of Positive Eigenvalues: 29
No. of Negative Eigenvalues: 4
Average distance to median:
gut left palm right palm tongue
0.3950 0.4991 0.5487 0.3160
Eigenvalues for PCoA axes:
(Showing 8 of 33 eigenvalues)
PCoA1 PCoA2 PCoA3 PCoA4 PCoA5 PCoA6 PCoA7 PCoA8
3.8480 2.6660 1.1788 0.8376 0.6125 0.5090 0.4639 0.4153 vegan::permutest(bd)
Permutation test for homogeneity of multivariate dispersions
Permutation: free
Number of permutations: 999
Response: Distances
Df Sum Sq Mean Sq F N.Perm Pr(>F)
Groups 3 0.28883 0.096278 9.0096 999 0.001 ***
Residuals 30 0.32059 0.010686
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Takeaway
- Ordination summarizes dissimilarity, not biology.
- The distance metric and preprocessing choices define the geometry.
- Visual separation is descriptive. Statistical tests support interpretation.
- Always check dispersion when using PERMANOVA.